All Paths from Source to Target

ID: 797

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

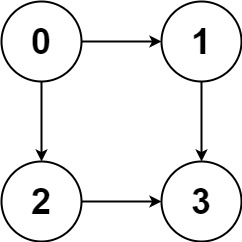
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Idea

DFS + Recursion

Start from the start node, do dfs on this node and if there's a valid path exists, add this path to result.

When a valid path found, add to result as a new ArrayList to prevent reference update in future operations

When done with dfs from a given node, remove the last element from the current path list to proceed on to other nodes

Code

public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
    List<List<Integer>> paths = new ArrayList<>();
    List<Integer> currPath = new ArrayList<>();
    dfs(graph, 0, graph.length-1, currPath, paths);
    return paths;
}    
boolean dfs(int[][] graph, int i, int target, List<Integer> currPath, List<List<Integer>> paths){
    currPath.add(i);
    if(i==target){
        return true;
    }
    for(int j: graph[i]){
        if(dfs(graph, j, target, currPath, paths)){
            paths.add(new ArrayList<>(currPath));
        };
        currPath.remove(currPath.size()-1);
    }
    return false;
}